문제:
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.

현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
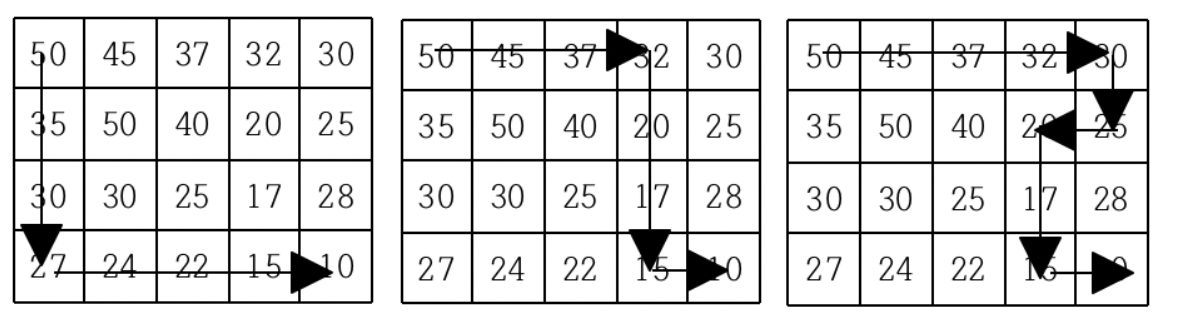
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력:
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력:
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.
풀이:
이 문제는 dfs 만 사용하면 안되는 문제이다. dfs만 사용하면 이미 탐색한 곳을 다시 탐색하여 시간초과가 난다. 탐색한곳을 탐색처리하면 다시 방문처리할 수 없어 안된다. dp를 통해 각 위치에서에 갈 수 있는 수를 저장해놓는식으로 해야한다.
M,N = map(int, sys.stdin.readline().split(" "))
maps = [list(map(int,sys.stdin.readline().rstrip().split(" "))) for _ in range(M)]
visited = [[ 0 ] * N for _ in range(M)]
start = maps[0][0]; end = maps[M-1][N-1]
move = [(1,0),( -1,0),(0,-1),(0,1)] #상,하,좌,우
dp = [[-1 for _ in range(N)] for _ in range(M)]
def dfs(x, y):
if x == M - 1 and y == N - 1:
return 1
if dp[x][y] == -1: # 탐색 안 했으면
dp[x][y] = 0 # 탐색 한걸로 만들어줌
for dx, dy in move:
nx = x + dx
ny = y + dy
if 0 <= nx < M and 0 <= ny < N:
if maps[x][y] > maps[nx][ny]:
dp[x][y] += dfs(nx, ny)
return dp[x][y]
print(dfs(0, 0))
dp 를 모든 부분은 -1 방문 안 했다고 처리를 해둔다.
그리고 탈출조건은 N-1,M-1 을 만났을때 탈출을 해준다.
똑같이 dfs를 돌리는데 만약에 dp[x][y] 가 탐색을 안 한 곳이면 0으로 만들어준다.
그리고 마지막에 dfs(nx,ny) 를 더해주는데 이 부분에서 깊게 들어가서 M-1,N-1 을 만나면 1을 리턴해준다.
즉 0,0 에서 3,4 를 가는 노선에 +1 을 해주는것이다.

처음 코드를 돌리면 저 선 부분이 다 0 으로 바뀌고 return을 받으면서 (0,0) ~(2,3) 까지 1로 바뀐다 (2,4) 는 도착지점이기때문에 바뀌지 않는다.
[[1, -1, -1, -1, -1], [1, -1, -1, -1, -1], [1, -1, -1, -1, -1], [1, 1, 1, 1, -1]]이런식으로 말이다.
그러면 리턴으로 쭉 돌아오면 다시 (0,0) 에 부분이다. 그리고 아까 포문으로 재귀를 불렀을텐데, 아직 실행 안 한 재귀가 실행된다.
그림에서 밑으로 간게 끝나 이제 오른쪽으로 갈 차례이므로 오른쪽으로 실행한다.
탐색한 곳이거나 탐색할 수 없으면 자기자신을 리턴하면 된다.
dp 어렵다





댓글