문제 바로가기
문제:
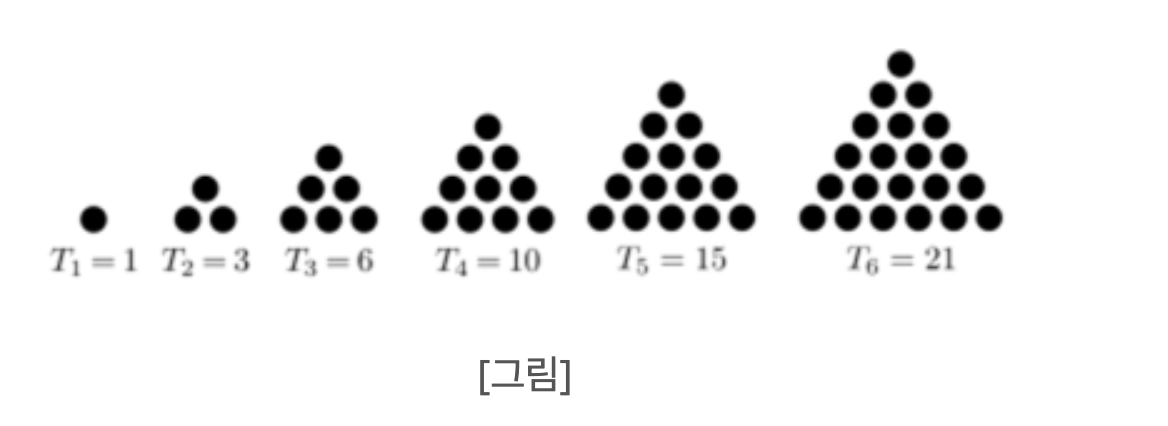
삼각수 Tn(n ≥ 1)는 [그림]에서와 같이 기하학적으로 일정한 모양의 규칙을 갖는 점들의 모음으로 표현될 수 있다. 자연수 n에 대해 n ≥ 1의 삼각수 Tn는 명백한 공식이 있다. Tn = 1 + 2 + 3 + ... + n = n(n+1)/2 1796년, 가우스는 모든 자연수가 최대 3개의 삼각수의 합으로 표현될 수 있다고 증명하였다. 예를 들어,
- 4 = T1 + T2
- 5 = T1 + T1 + T2
- 6 = T2 + T2 or 6 = T3
- 10 = T1 + T2 + T3 or 10 = T4
이 결과는 증명을 기념하기 위해 그의 다이어리에 “Eureka! num = Δ + Δ + Δ” 라고 적은것에서 유레카 이론으로 알려졌다. 꿍은 몇몇 자연수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 궁금해졌다. 위의 예시에서, 5와 10은 정확히 3개의 삼각수의 합으로 표현될 수 있지만 4와 6은 그렇지 않다. 자연수가 주어졌을 때, 그 정수가 정확히 3개의 삼각수의 합으로 표현될 수 있는지 없는지를 판단해주는 프로그램을 만들어라. 단, 3개의 삼각수가 모두 달라야 할 필요는 없다.
입력:ㅌ
프로그램은 표준입력을 사용한다. 테스트케이스의 개수는 입력의 첫 번째 줄에 주어진다. 각 테스트케이스는 한 줄에 자연수 K (3 ≤ K ≤ 1,000)가 하나씩 포함되어있는 T개의 라인으로 구성되어있다.
출력:
프로그램은 표준출력을 사용한다. 각 테스트케이스에대해 정확히 한 라인을 출력한다. 만약 K가 정확히 3개의 삼각수의 합으로 표현될수 있다면 1을, 그렇지 않다면 0을 출력한다.
풀이:
import sys
sys.stdin = open('/Users/song/Desktop/Python/Python/h.txt', 'r')
T = int(sys.stdin.readline())
def find(n):
for i in range(len(lst)):
for j in range(i, len(lst)):
for k in range(j, len(lst)):
if lst[i]+lst[j]+lst[k] == n:
return 1
return 0
lst = [1]
for i in range(2,45):
lst.append(lst[-1]+i)
for _ in range(T):
n = int(input())
print(find(n))
이 문제는 브루트포스 문제이다. 브루트포스란. 구조를 전체적으로 탐색하는 방법이다. 무식하게 탐색하는것이다,
lst 에 삼각형에 합들을 다 나열해주고
lst의 3개의 삼각형으로 만든다고 했으니 for문 3개로돌려준다.
123, 124,125... 이런식 그러다가 합이 맞으면 1 리턴





댓글