플로이드-워셜 알고리즘

플로이드 워셜 알고리즘이란 

모든 최단경로를 구하는 알고리즘이다.

다익스트라는 하나의 정점에서 다른 모든 정점까지의 최단 거리를 구하는 알고리즘(S.S.S.P - Single Source Shortest Path) 이었다면,

플로이드-워셜 알고리즘은 한 번 실행하여 모든 노드 간 최단 경로를 구할 수 있다

 

한붓그리기인 오일러서킷 과는 다르다

오일러 서킷은 그래프의 모든 간선을 정확히 한 번씩 지나서 시작점으로 돌아오는 경로를 말한다. 반드시 시작점으로 돌아와야하며, 한 번 지나간 선으로는 지나가지 않고 모든 선을 이어 그림을 완성하는 것이다. 나중에 오일러 서킷을 알아보도록 하겠다.

 

플로이드 - 워셜 알고리즘은 O(N^3) 이기 때문에 N이 20 만 넘어가도 엄청나게 된다.

 

모든 노드 간의 최단거리를 구해야 하므로 2차원 인접행렬로 만든다.

그리고 자기자신은 0 으로 표현할 수 있다.

 

INF = int(1e9)
graph = [[INF] * (n + 1) for _ in range(n + 1)]

for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0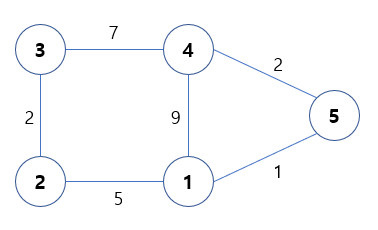

플로이드- 워셜

이 문제로 예시를 들어보겠다.

 

만약 2에서 4 로 가는방법은

2 > 3 > 4 도 가능하고

2> 1 > 4 도 가능하고

2 > 1 > 4 > 5 등등 가능하다.

이것을 코드로 표현하면 이렇게 된다.

# 2. 플로이드 - 와샬 알고리즘
for k in range(1, n + 1): # 경유지
    for a in range(1, n + 1): # 출발지
        for b in range(1, n + 1): # 도착지
            # a > b 랑 a > k > b중에  최솟값으로 바꿔줌
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

k가 1일때 

1 을 경유하여

a에서 b 까지 가는경우

 

k가 2일때

2 를 경유하여 a 에서 b를 가는경우 

이런식으로 하나하나 다 체크한다.

 

모든 노드들을 중간 노드로 선정하는 과정을 각 라운드마다 거친다.

 

 

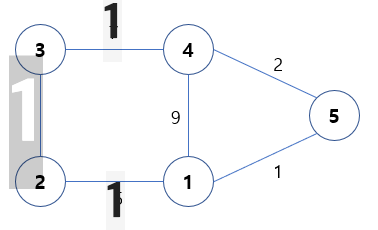
만약 이렇게 바뀌었다고 생각해보고 저위에 코드를 봐보자.

만약 1 > 4 를 생각하면

1> 4 보다 1>2>3>4 가 더 최솟값이다.

 

근데 1>2>3>4 가 나오려면 1>2 ,2>3, 3>4 를 다 알아야한다.

그래서 경유지인 k를 사용하여 1부터 돌리면서

k가2 일때  1>2>3 를 알게되는데 즉 1> 3 가는 최선 방법이다.

 

그리고 k 가 3 이 되면

 1> 경유지3 > 4 으로 진행이 된다.

 

 

그걸 코드로 옮겨와서 확인하면 아래와 같다.

 

k = 2 일때 graph[1][3] 을 알게된다. 1> 2> 3

 

k = 3 일때 graph[1][4] 을 알게된다. 1 >3>4

근데 k = 2일때 graph[1][3] 을 구해뒀다.

 

좀 말이 어려운데,, 따라가면서 하면 이해가 될 수 있다..

 

 

관련문제

https://windy7271.tistory.com/entry/Python%F0%9F%A5%875%EB%B0%B1%EC%A4%80%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-21278%EB%B2%88-%ED%98%B8%EC%84%9D%EC%9D%B4-%EB%91%90-%EB%A7%88%EB%A6%AC-%EC%B9%98%ED%82%A8

(Python/🥇5)백준알고리즘 21278번: 호석이 두 마리 치킨

https://windy7271.tistory.com/entry/Python%F0%9F%A5%873%EB%B0%B1%EC%A4%80%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-11404-%ED%94%8C%EB%A1%9C%EC%9D%B4%EB%93%9C

(Python/🥇3)백준알고리즘 11404 플로이드